フィボナッチは、13世紀のイタリア人数学者レオナルド・フィボナッチが発見した数列です。
このフィボナッチ数列と、数列から計算されるフィボナッチ比率は、一見無秩序な動きと思える自然界の各所で観察されています。
ならば、自然界と同じように一見無秩序に思えるマーケットの値動きも、フィボナッチ数列の法則が応用できるのではないかと考えられています。
1.フィボナッチ数列
2.フィボナッチ数列と黄金比
3.フィボナッチリトレースメント
4.フィボナッチエキスパンション
1.フィボナッチ数列
1,1,2,3,5,8,13,21,34,55,89,144,233,377,・・・・・・・・
この数列の規則性は、はじめの2つの1を除いたこの数列のそれぞれの数は、その1つ前の数と2つ前の数との和になっています。
1+1=2、1+2=3、2+3=5、3+5=8、5+8=13、・・・・・・
このような数列をフィボナッチ数列といいます。
このフィボナッチ数列の数字は自然界に多く見られます。
1:花の花弁の枚数は3枚、5枚、8枚、13枚のものが多く見られます
2:ヒマワリの種の並び方はらせん状に21個、34個、55個、89個、・・・と並んでいます
3:松ぼっくりやパイナップルのかさを良く観察すると右回りに8個ずつ、左回りに5個ずつ、または、右回りに5個ずつ、左回りに3個ずつになっています。
2.フィボナッチ数列と黄金比
フィボナッチ数列の隣り合う数値で、または、1つ空けた隣の数値で比率を求めてみましょう。
隣り合う上位の数値に対する比率は、0.618に近づいていきます。(右側の数値で除算)
8÷13=0.6153、13÷21=0.619、21÷34=0.6176、34÷55=0.6181
隣り合う下位の数値に対する比率は、1.618に近づいていきます。(左側の数値で除算)
13÷8=1.625、21÷13=1.6153、34÷21=1.619、55÷34=1.6176
0.618と1.618は【黄金分割比】と呼ばれ、古来から、建築、彫刻、デザインの分野、最近の身近なものではクレジットカード等、美しいと感じるデザインの中の数値の比率を求めてみると現れる比率です。
2つ上位の数値に対する比率は、0.382に近づいていきます。(1つ空けた右側の数値で除算)
8÷21=0.3809、13÷34=0.3823、21÷55=0.3818、34÷89=0.382
2つ下位の数値に対する比率は、2.618に近づいていきます。(1つ空けた左側の数値で除算)
13÷5=2.6、21÷8=2.2525、34÷13=2.615、55÷21=2.619
3つ上位の数値に対する比率は、0.236に近づいていきます。(2つ空けた右側の数値で除算)
8÷34=0.2352、13÷55=0.2363、21÷89=0.2359、34÷144=0.2361
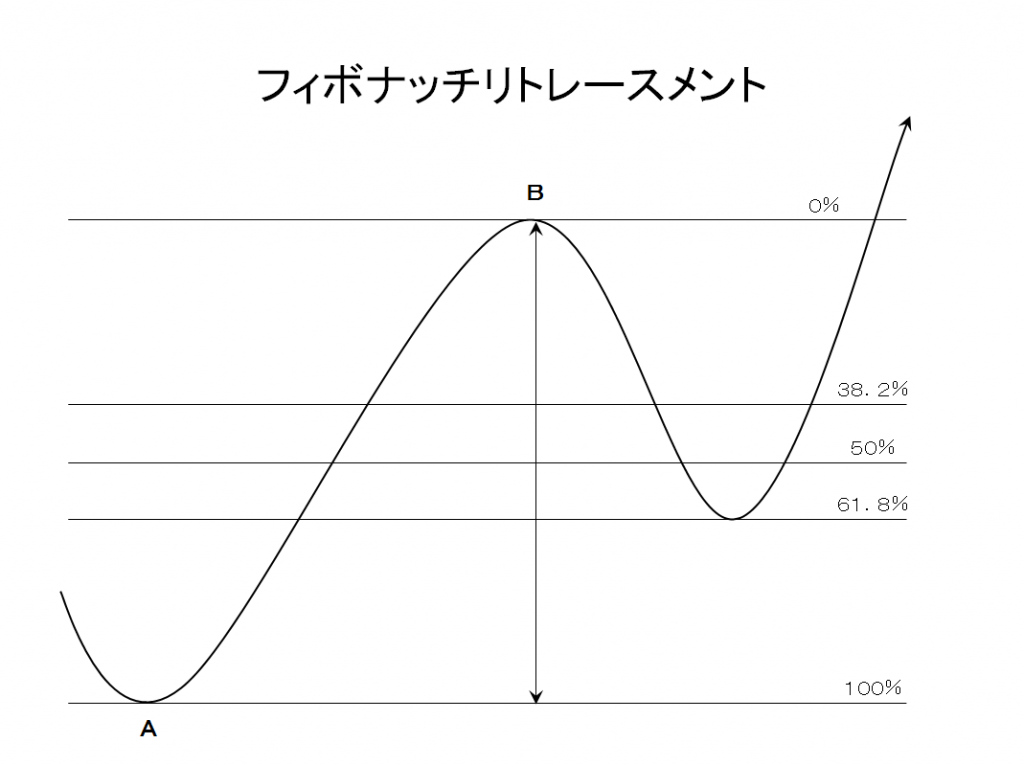
3.フィボナッチリトレースメント
トレンドは一直線に上昇することは極めてまれで、必ず上下の波動を伴って、上昇しては調整の下げを見せて再度上昇して行きます。
フィボナッチリトレースメントは、調整の下げがどの価格までになるだろうか、調整の戻りがどの価格になるだろうかを、フィボナッチ比率を応用して推測しようというテクニカル分析手法です。
フィボナッチリトレースメントは戻りの価格を比率で計算する手法です。
戻りの比率として主な比率は、38.2%、50%、61.8%です。
補助的に、23.6%と76.4%を使用するパターンもあります。
強いトレンドにおいては、最小の戻しはだいたい38.2%です。弱いトレンドにおいては最大の戻し幅は61.8%です。
特に強いトレンドにおいては、23.6%辺りが最初の戻しの目途になる場合もあります。
また、ボラティリティー(値動きの大きさ)が大きい通貨ペアなどでは76.4%辺りが最大の戻し幅になる場合もあります。
MT4のフィボナッチリトレースメントの使用方法はこちらをご覧ください。
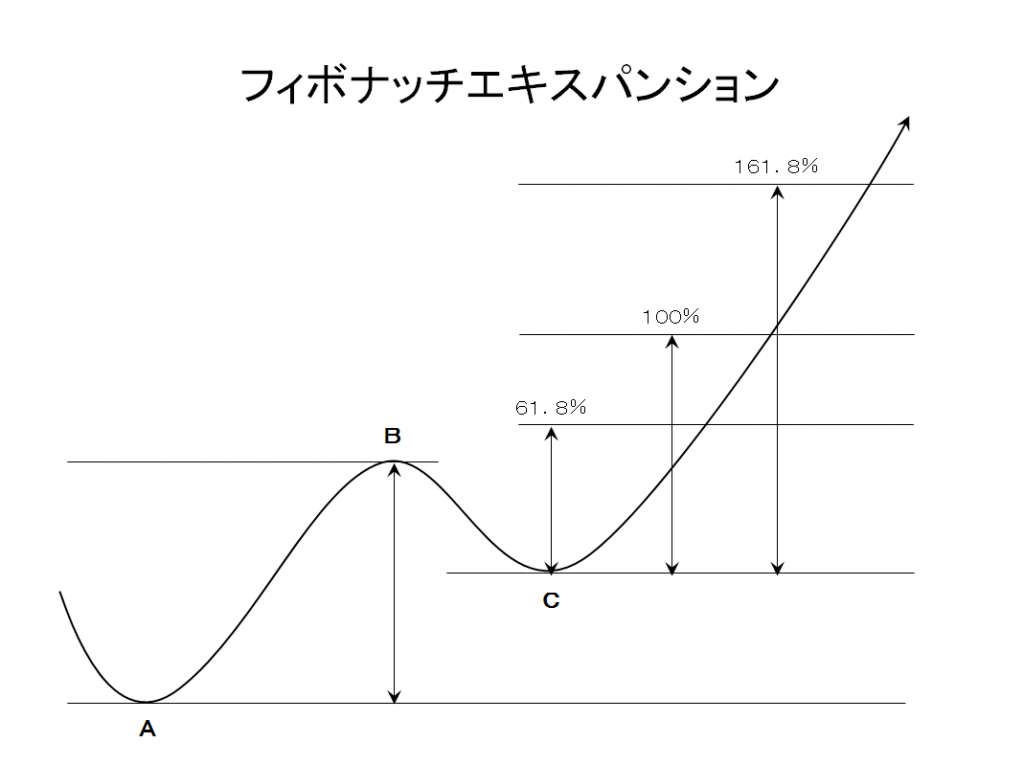
4.フィボナッチエクスパンション
フィボナッチエクスパンションは、上昇トレンドを例に取ると、上昇トレンドの上昇幅と押し目の価格を基準として、高値を更新した時に、どのくらい高値を更新するかをフィボナッチ比率をもとに計算する手法です。
主に、利益確定のターゲットをどこに置くべきかを判断するのにつかわれます。
上昇トレンド波動の上昇幅を100%ととして、押し目の価格から、比率で計算した価格をターゲット価格とします。
ターゲットを計算する割合として、61.8%、100%、161.8%が主に使われます。
レベルの追加例として、123.6%、138.2%を追加することもあります。
MT4のフィボナッチエキスパンションの使用方法はこちらをご覧ください。